Computational modelling of a bouncing ball using differential equations of motion

Using differential equations of motion (EOMs) governed by Newton’s 2^nd law we can describe the dynamics and kinematics of objects in motion. In this post I describe how EOMs can be calculated and applied programmatically for a simple case of a falling and bouncing ball with one translational degree of freedom - i.e. a ball bouncing perfectly perpindicular to the ground plane with no rotational component.

Defining the equations of motion

We can split the problem up into two phases, where phase 1 involves the ball in freefall. Here the equation of motion is governed by gravitational force, and air resistance.

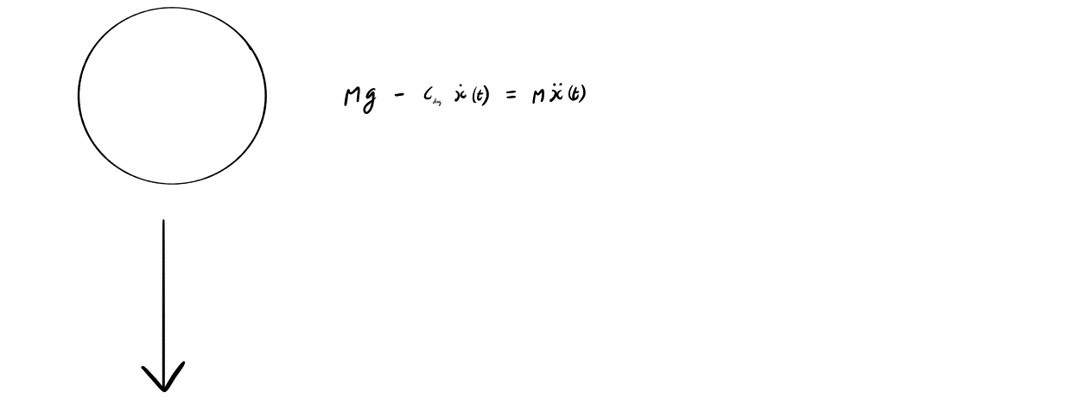
In phase 2 we consider the contact/impact between the ball and the ground surface as an unforced mass-spring-damper model. Given appropriate model parameters, this kind of model can accurately represent overall impact/contact behaviour. We make the assumption that the ball is a rigid body that does not deform, and x_pen(t) is the ground displacement in the contact phase (i.e. the penetration).

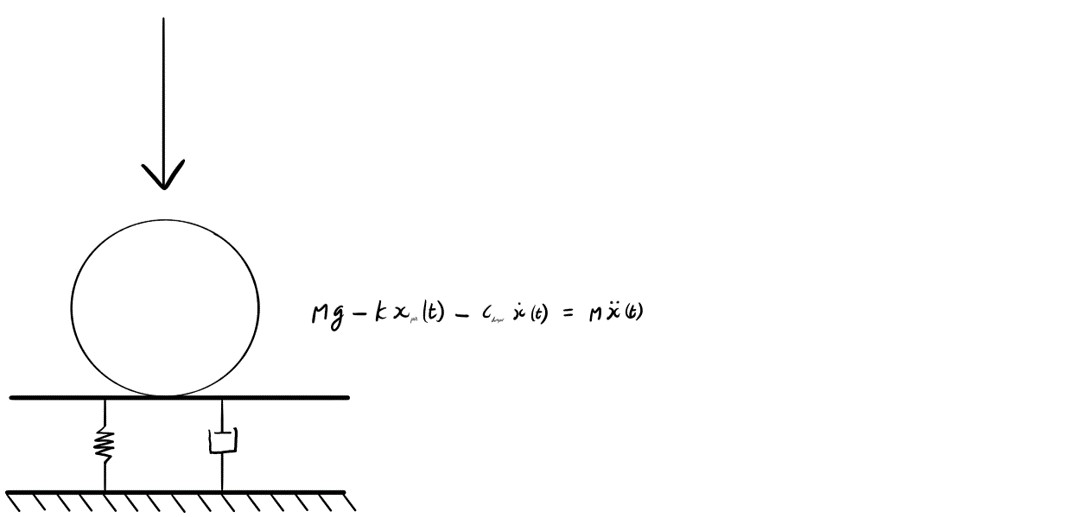
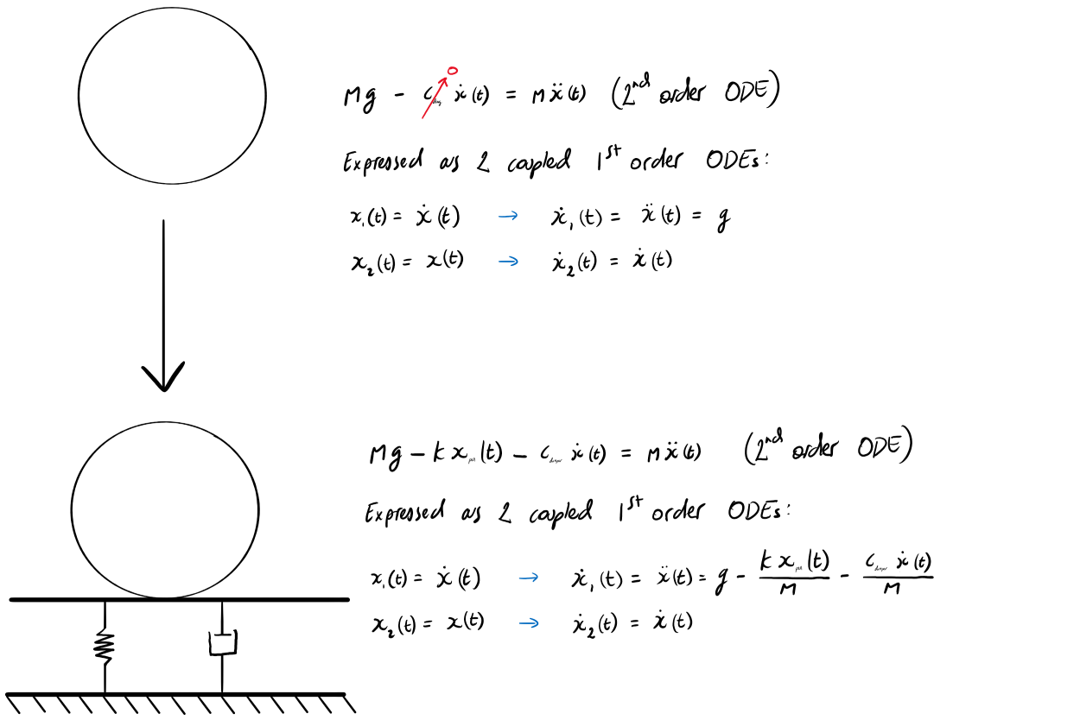
Numerical integration of ordinary differential equations

Since each of the the EOMs (for both phase 1 and phase 2) are in the form of a 2^nd order ordinary differential we apply a Runge-Kutta numerical integration approach. First, we need to simply the EOMs to the form of coupled 1^st order equations i.e. x₁(t), and x₂(t). To simplify the problem further we will disregard the effect of air resistance, i.e. set c_drag to zero.

Specifically we apply the Matlab ode23 function, which is an implementation of an explicit Runge-Kutta (2,3) pair of Bogacki and Shampine. There are other ODE solvers available in Matlab, for example ode45, which is a higher order method. For this simplified example the ode23 function is used as it is more computationally efficient.

Implementation

The full code is available here.

main.m

close all; clear

%simulation of bouncing ball
global g k c m h r

% set parameter values
g = 9.81;k = 5000; c=5; m = 0.2; h=0.2; r = 0.01;

%set integration time interval, and maximum time step
tspan = [0 2];
tstep = 1e-3;

%set initial conditions: velocity and displacement
X0 = [0  0];

%call ode23 function and feed relevant inputs
OPTIONS = odeset('MaxStep',tstep); %set max integration timestep
[tout,xout] = ode23('ball',tspan,X0,OPTIONS);

ball.m

function xdot  = ball(t,x)

global g k c m h r

xdot  = zeros(2,1);

%determine if penetration has occured
pen = (x(2) + r) - h; %compute penetetration for contact

if pen <0 
    xdot(1) = g; xdot(2)  = x(1);
else xdot(1) = g - ((k*pen)/m) -((c*x(1))/m); xdot(2)  = x(1);

end

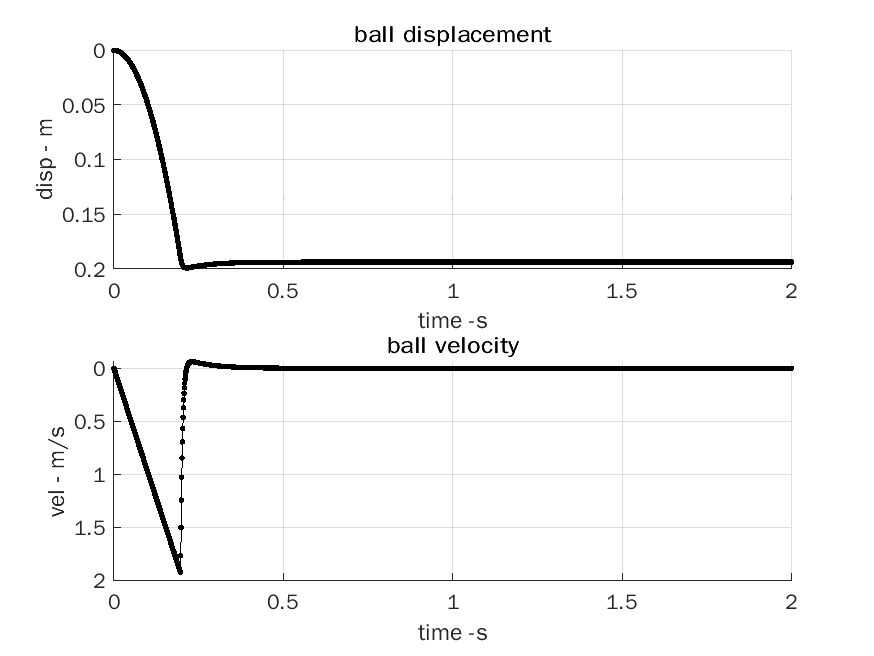
We would like to model a ball of mass 0.2kg, and radius 0.01m. For reference, we choose nominal values for the spring constant (k) and and damping constant (c) i.e. k=5,000, and c=5.

Reference

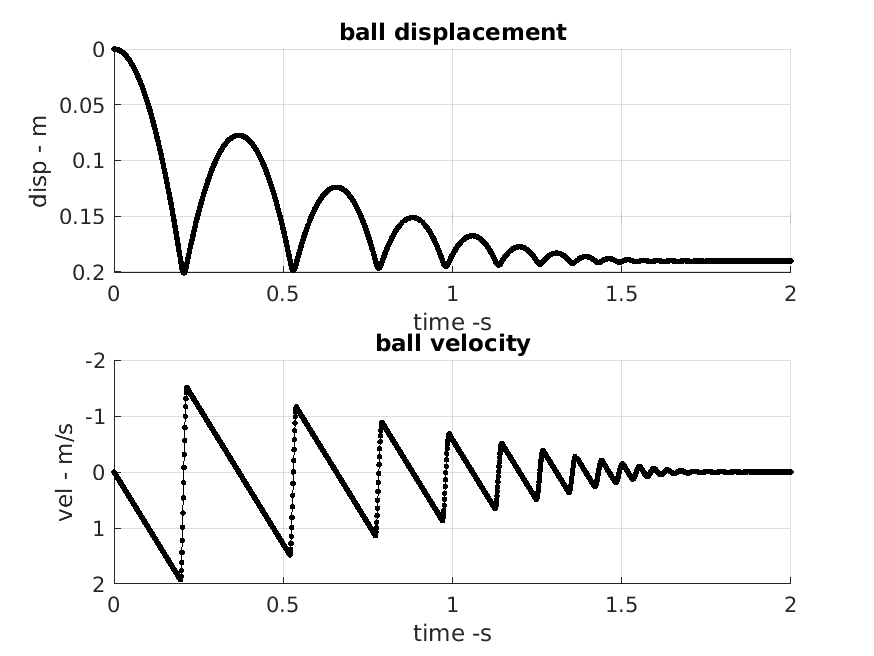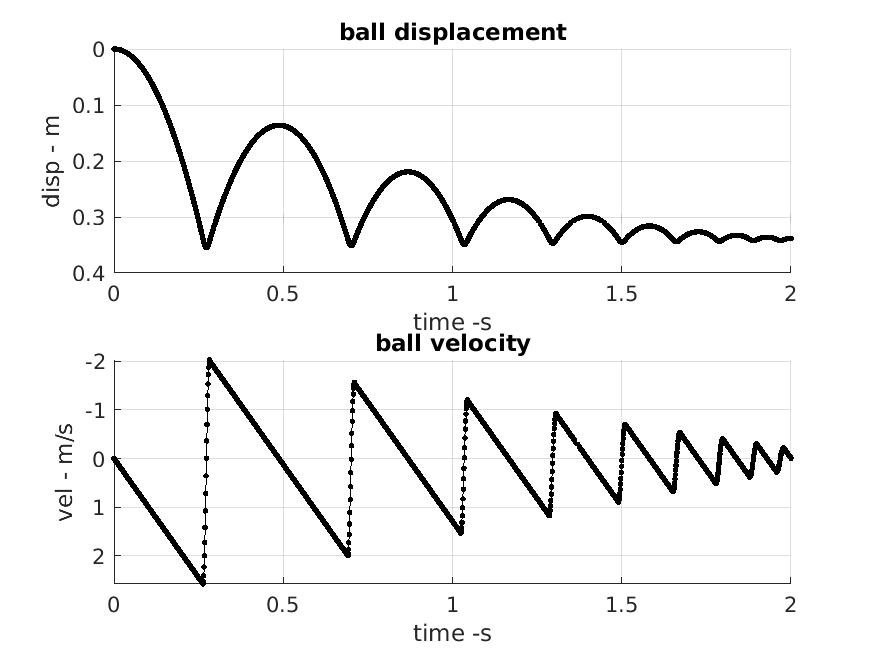
Effect of changing the drop height.

h=0.35m

Effect of adding an initial velocity to the ball.

v=-1 m/s

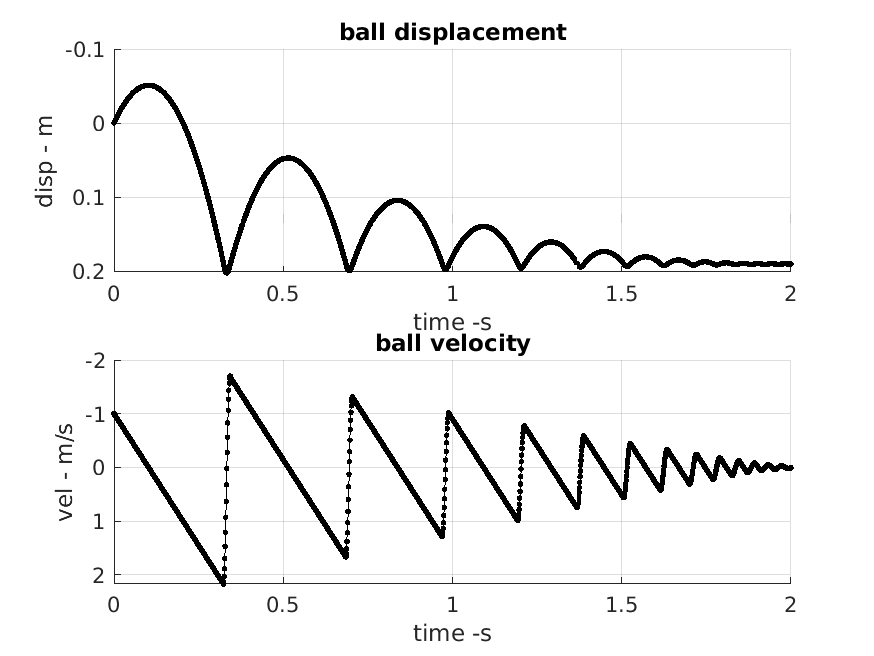Effect of changing the mass and size of the ball.

m=0.5kg, r=0.08m

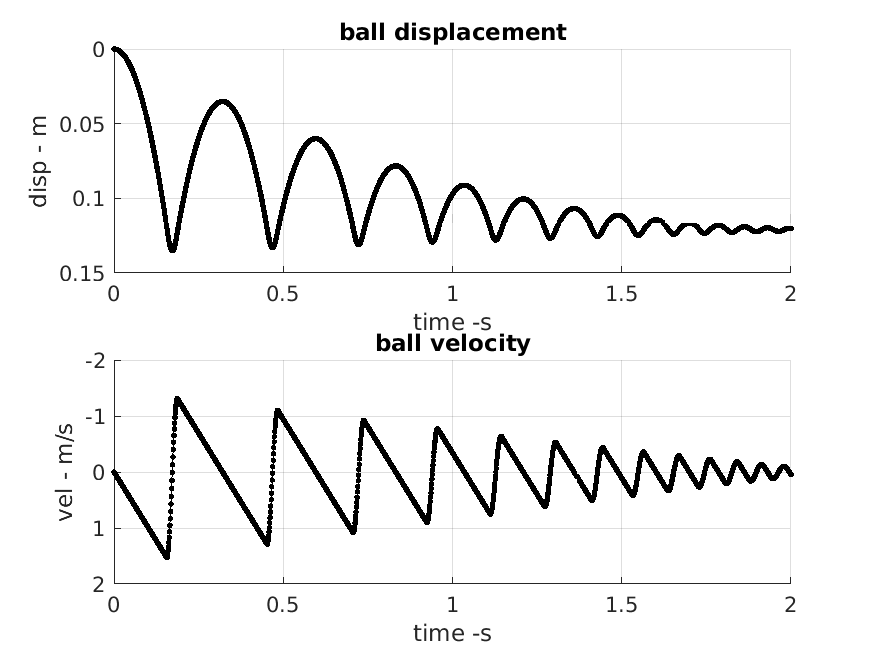Effect of the gravitational environment.

The Moon:	g=1.62m/s/s

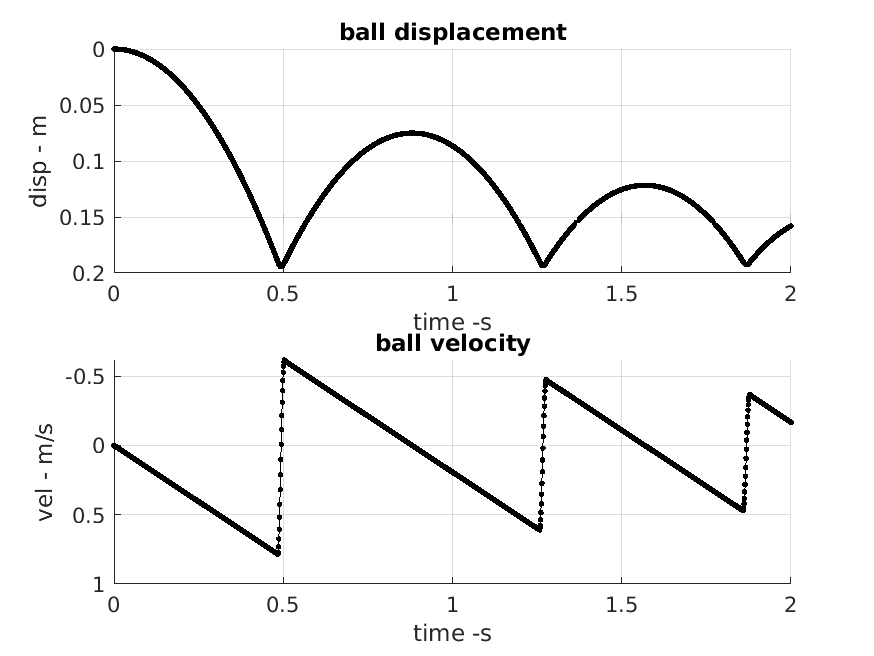Effects of varying parameters k and c on oscillatory behaviour.

% under-damped:
c=sqrt(4*m*k)-(9/10)*sqrt(4*m*k)

% critically damped:
c=sqrt(4*m*k)

% over-damped:
c=sqrt(4*m*k)+(9/10)*sqrt(4*m*k)

Under-damped:	c < sqrt(4mk)

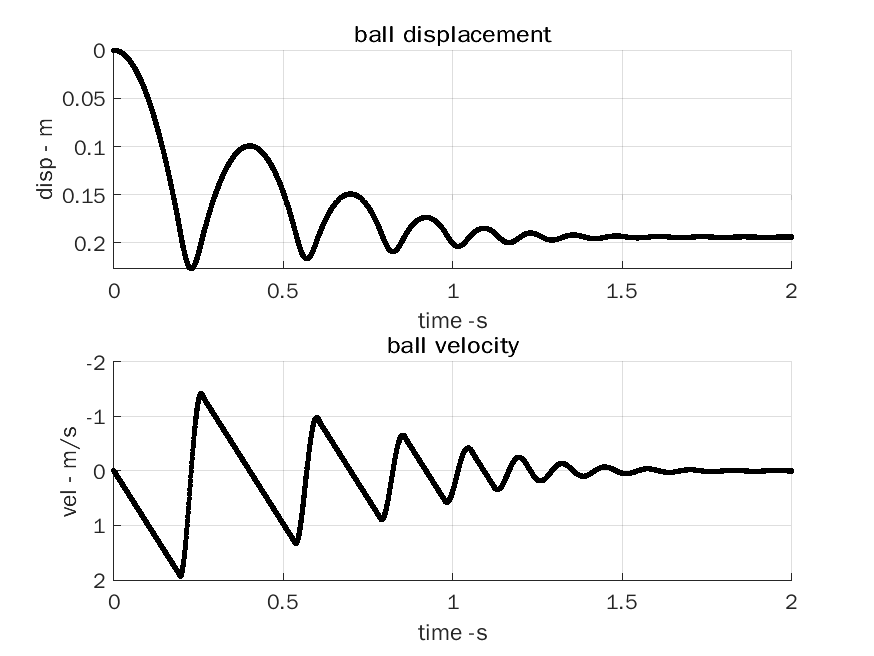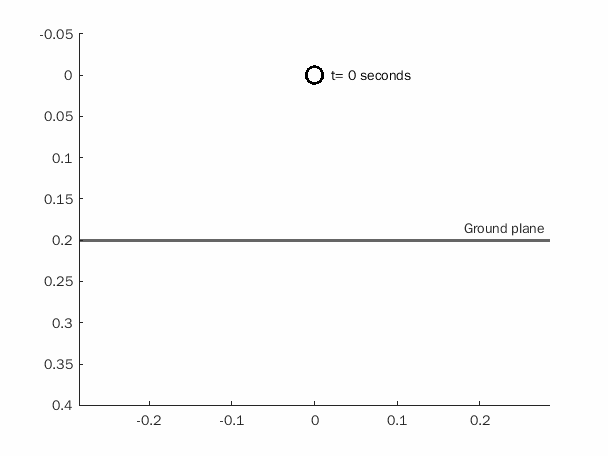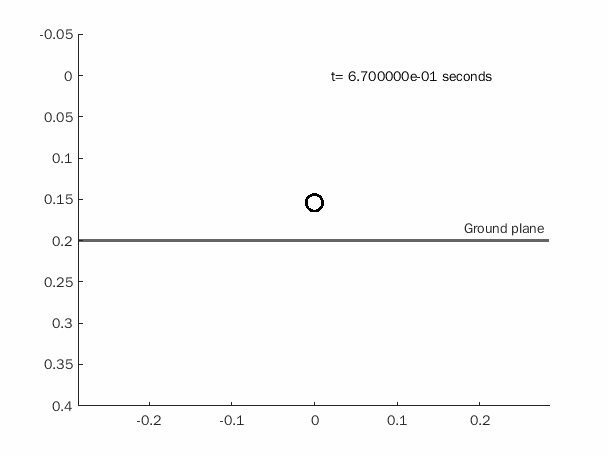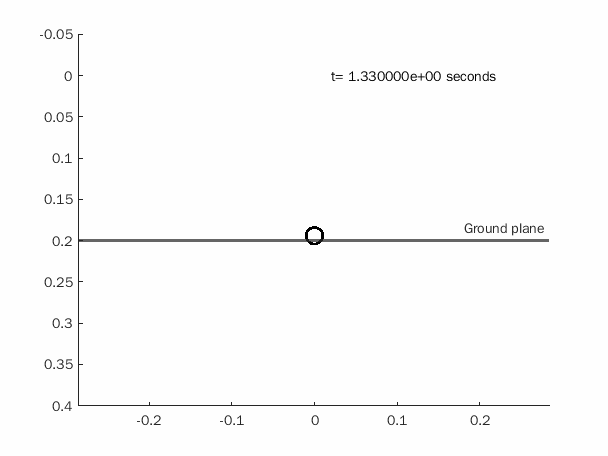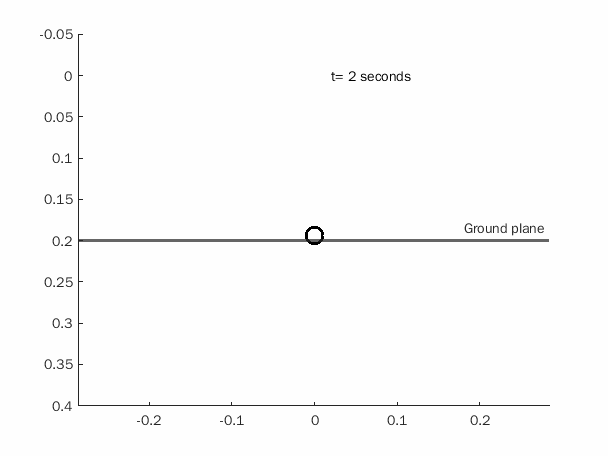
Critically damped:	c = sqrt(4mk)

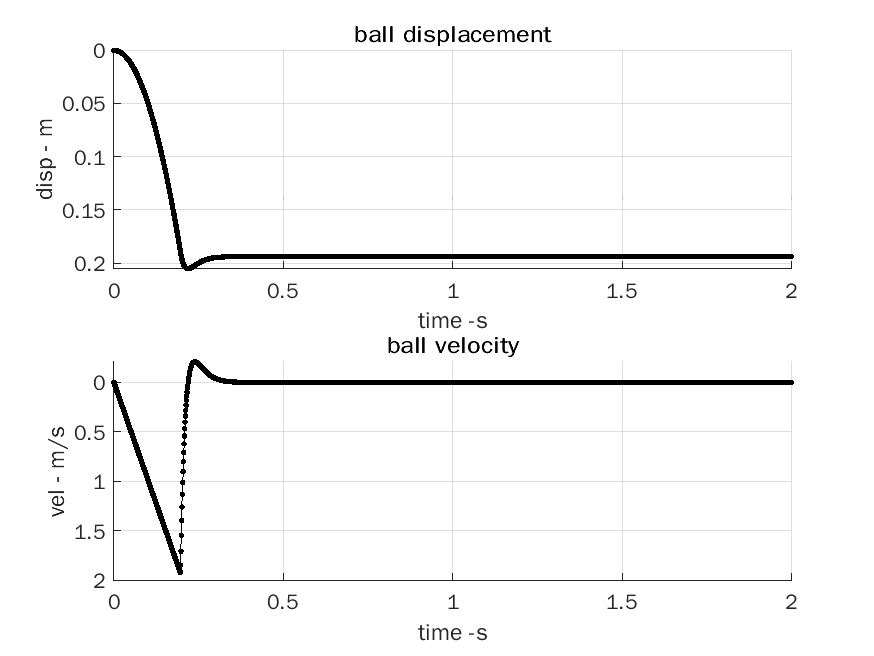Over-damped:	c > sqrt(4mk)

Implications

In this post I have developed a physics simulation/computational model of a bouncing ball. Relationships between system parameters and the motion of a dropped ball are investigated, namely, the drop height, initial velocity, ball mass, ball size, and the ground surface stiffness and damping coefficient. Exploring this code and varying parameters may allow the user gain an understanding of the effects of contact characteristics.