Tutorial 3: 3D rotations
Solutions:
Q1
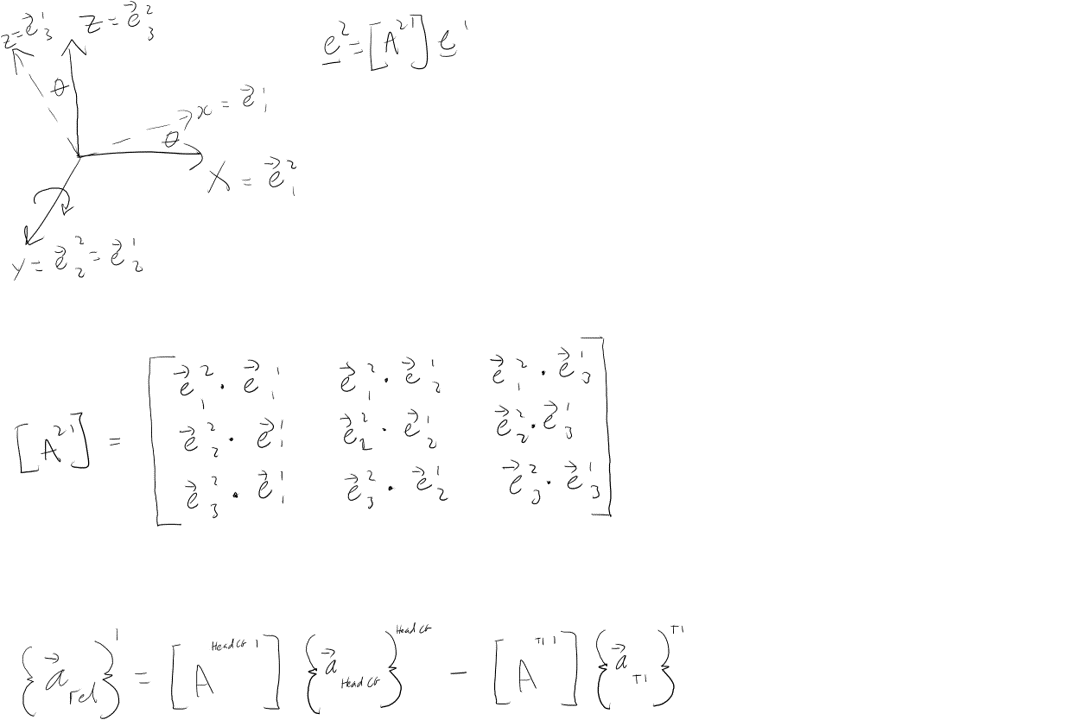
# Dependencies
from math import sqrt
import matplotlib.pyplot as plt
import numpy as np
import mpl_toolkits.mplot3d as plt3d
from pyquaternion import Quaternion
def RotationY(θy):
""" Calculate a rotation matrix for a rotation about the Y axis"""
ROTMy = np.array([[np.cos(θy),0,np.sin(θy)],
[0,1,0],
[-np.sin(θy),0,np.cos(θy)]])
return ROTMy
fig = plt.figure(1)
ax = fig.add_subplot(111, projection='3d')
fig.suptitle('4B17 Week 3 tutorial – 3D Rotations: Q1', fontsize=12)
# Plot the global coordinate system
dirxglobal=[1,0,0]
diryglobal=[0,1,0]
dirzglobal=[0,0,1]
ax.quiver(0,0,0,dirxglobal[0],dirxglobal[1],dirxglobal[2],color='r')
ax.quiver(0,0,0,diryglobal[0],diryglobal[1],diryglobal[2],color='g')
ax.quiver(0,0,0,dirzglobal[0],dirzglobal[1],dirzglobal[2],color='b')
# Plot T1
aT1_pos = np.array([5,5,5])
T1_local = RotationY(np.radians(-15)) @ np.array([[1,0,0],[0,1,0],[0,0,1]])
dirxlocal=T1_local @ [1,0,0]
dirylocal=T1_local @ [0,1,0]
dirzlocal=T1_local @ [0,0,1]
ax.quiver(aT1_pos[0],aT1_pos[1],aT1_pos[2],dirxlocal[0],dirxlocal[1],dirxlocal[2],color='r')
ax.quiver(aT1_pos[0],aT1_pos[1],aT1_pos[2],dirylocal[0],dirylocal[1],dirylocal[2],color='g')
ax.quiver(aT1_pos[0],aT1_pos[1],aT1_pos[2],dirzlocal[0],dirzlocal[1],dirzlocal[2],color='b')
aT1_global=T1_local @ np.array([110,-4,80])
aT1_hat = aT1_global / np.linalg.norm(aT1_global)
ax.quiver(aT1_pos[0],aT1_pos[1],aT1_pos[2],aT1_hat[0],aT1_hat[1],aT1_hat[2],color='black')
ax.text(aT1_pos[0]+aT1_hat[0],aT1_pos[1]+aT1_hat[1],aT1_pos[2]+aT1_hat[2], '%s' % (r'$\vec a_{T1}$'), size=12, zorder=1,color='black')
# Plot HeadCG
aheadCG_pos = np.array([2,5,8])
headCG_local = RotationY(np.radians(-30)) @ np.array([[1,0,0],[0,1,0],[0,0,1]]) # RENAME
dirxlocal=headCG_local @ [1,0,0]
dirylocal=headCG_local @ [0,1,0]
dirzlocal=headCG_local @ [0,0,1]
ax.quiver(aheadCG_pos[0],aheadCG_pos[1],aheadCG_pos[2],dirxlocal[0],dirxlocal[1],dirxlocal[2],color='r')
ax.quiver(aheadCG_pos[0],aheadCG_pos[1],aheadCG_pos[2],dirylocal[0],dirylocal[1],dirylocal[2],color='g')
ax.quiver(aheadCG_pos[0],aheadCG_pos[1],aheadCG_pos[2],dirzlocal[0],dirzlocal[1],dirzlocal[2],color='b')
aheadCG_global=headCG_local @ np.array([250,5,20])
aheadCG_hat = aheadCG_global / np.linalg.norm(aheadCG_global)
ax.quiver(aheadCG_pos[0],aheadCG_pos[1],aheadCG_pos[2],aheadCG_hat[0],aheadCG_hat[1],aheadCG_hat[2],color='black')
ax.text(aheadCG_pos[0]+aheadCG_hat[0],aheadCG_pos[1]+aheadCG_hat[1],aheadCG_pos[2]+aheadCG_hat[2], '%s' % (r'$\vec a_{HeadCG}$'), size=12, zorder=1,color='black')
# Axis limits and lables
ax.set_xlim3d(-2,10)
ax.set_ylim3d(-2,10)
ax.set_zlim3d(-2,10)
ax.set_xlabel('Global X')
ax.set_ylabel('Global Y')
ax.set_zlabel('Global Z')
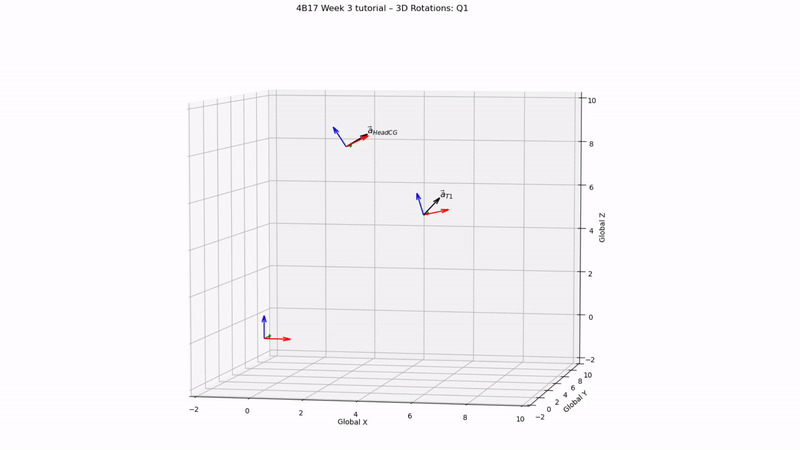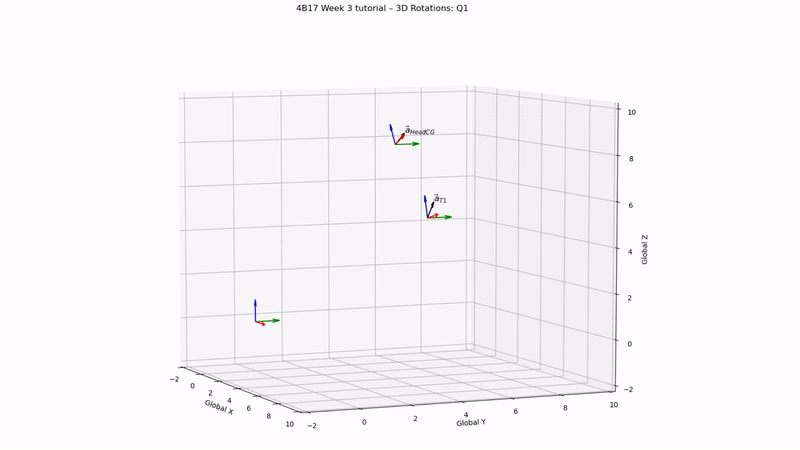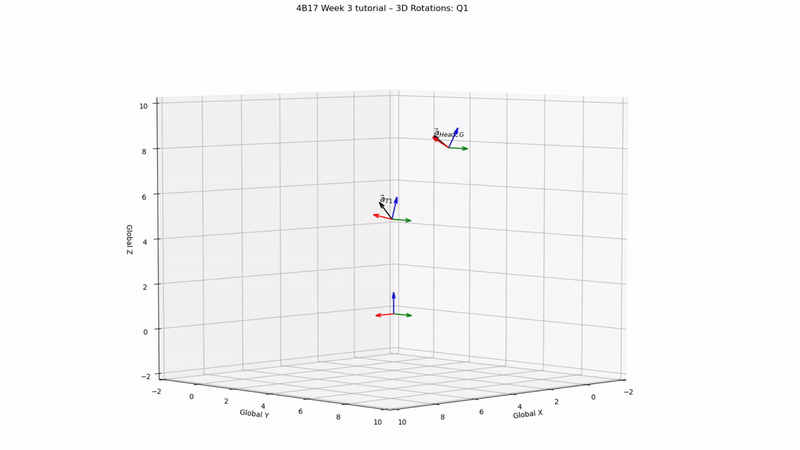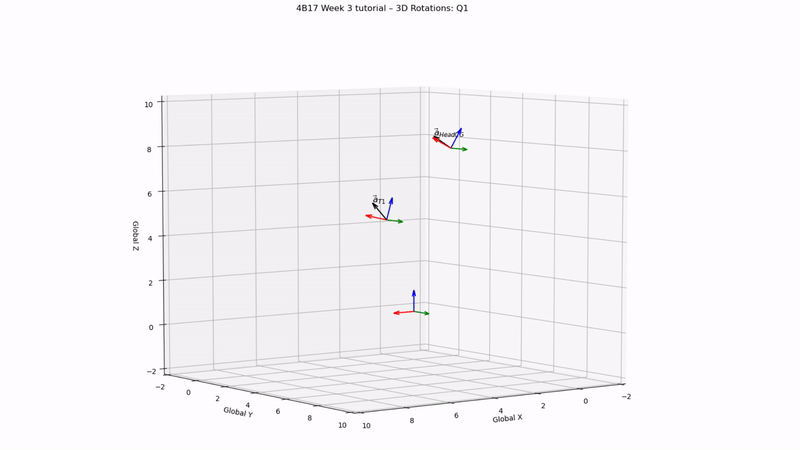
# Compute relative acceleration head CG and T1
a_rel_global = aheadCG_global - aT1_global
print('Q1 answer:', a_rel_global)
plt.show()
Q1 answer:
[120.96 9.00 36.58]
Q2
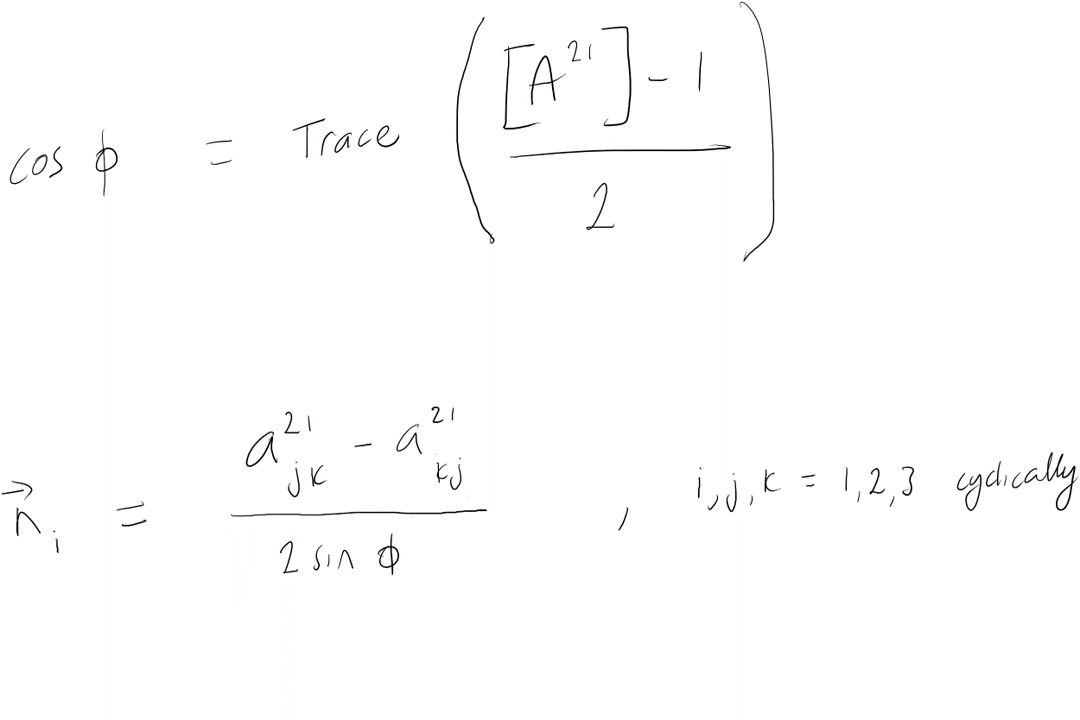
def Screw(ROTM):
""" Calculate the screw angle and axis for a given rotation matrix"""
n=[]
θ = np.arccos((np.trace(ROTM)-1)/2)
n.append(np.array(ROTM[1][2]-ROTM[2][1])/(2*np.sin(θ)))
n.append(np.array(ROTM[2][0]-ROTM[0][2])/(2*np.sin(θ)))
n.append(np.array(ROTM[0][1]-ROTM[1][0])/(2*np.sin(θ)))
return θ, n
# Aside: Screw axes and angles from Q1
θ,n = Screw(headCG_local)
print('headCG_local: screw angle = ', np.degrees(θ), 'screw axis = ',n)
θ,n = Screw(T1_local)
print('T1_local: screw angle = ', np.degrees(θ), 'screw axis = ',n)
A21 = np.array([[0.3584,0.8613,-0.3603],[-0.6638,0.5064,0.5503],[0.6564,0.0420,0.7532]])
θ,n = Screw(A21)
print('Q2 answer: screw angle = ', np.degrees(θ), 'screw axis = ',n)
fig = plt.figure(2)
ax = fig.add_subplot(111, projection='3d')
fig.suptitle('4B17 Week 3 tutorial – 3D Rotations: Q2', fontsize=12)
dirxlocal=[1,0,0]
dirylocal=[0,1,0]
dirzlocal=[0,0,1]
ax.quiver(0,0,0,dirxlocal[0],dirxlocal[1],dirxlocal[2],color='r',linestyle='--',label='original X axis')
ax.quiver(0,0,0,dirylocal[0],dirylocal[1],dirylocal[2],color='g',linestyle='--',label='original Y axis')
ax.quiver(0,0,0,dirzlocal[0],dirzlocal[1],dirzlocal[2],color='b',linestyle='--',label='original Z axis')
dirxlocal=A21@[1,0,0]
dirylocal=A21@[0,1,0]
dirzlocal=A21@[0,0,1]
ax.quiver(0,0,0,dirxlocal[0],dirxlocal[1],dirxlocal[2],color='r',label='reoriented X axis')
ax.quiver(0,0,0,dirylocal[0],dirylocal[1],dirylocal[2],color='g',label='reoriented Y axis')
ax.quiver(0,0,0,dirzlocal[0],dirzlocal[1],dirzlocal[2],color='b',label='reoriented Z axis')
# Plot screw axis and angle
ax.quiver(0,0,0,n[0],n[1],n[2],color='orange',linestyle='--',label='screw axis')
ax.text(0,0,0, ' θ = '+str(round(np.degrees(θ)))+'°', size=12, zorder=1,color='orange')
# Axis limits and lables and legend
ax.set_xlim3d(-2,2)
ax.set_ylim3d(-2,2)
ax.set_zlim3d(-2,2)
ax.set_xlabel('Global X')
ax.set_ylabel('Global Y')
ax.set_zlabel('Global Z')
ax.legend()
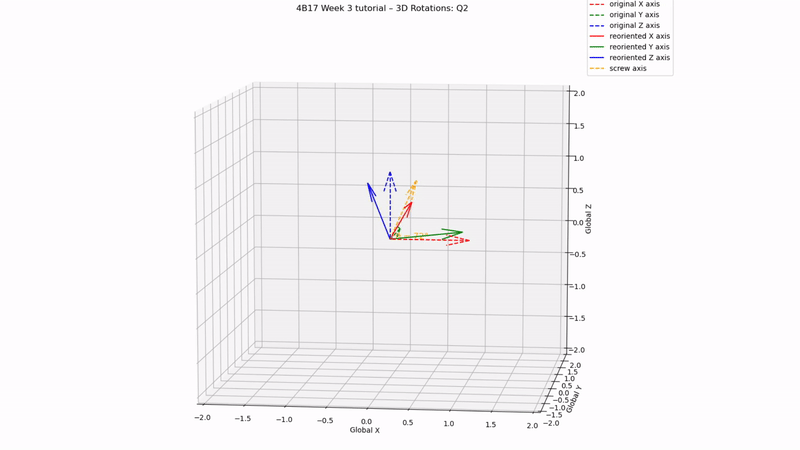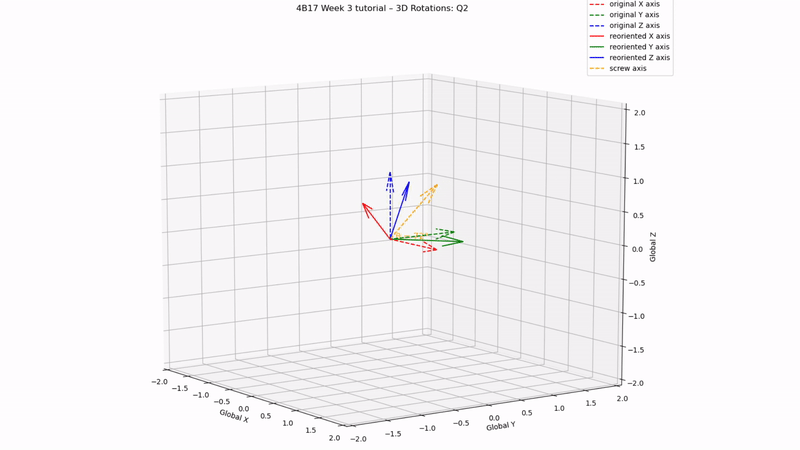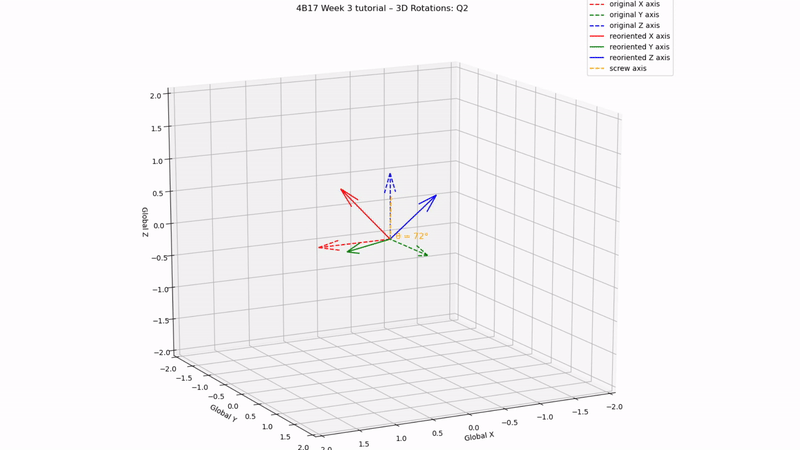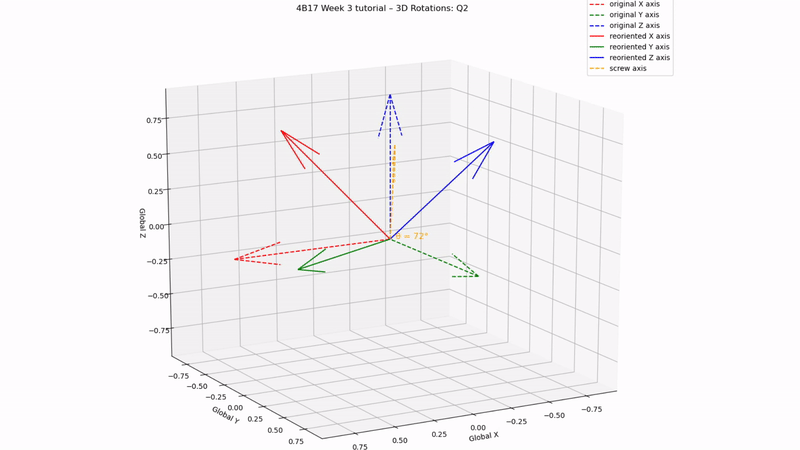
Screw axes and angles from Q1:
headCG_local:
screw angle = 30, screw axis = [0,1,0]
T1_local:
screw angle = 15, screw axis = [0,1,0]
Q2 answer:
screw angle = 72, screw axis = [0.27, 0.53, 0.80]
Q3
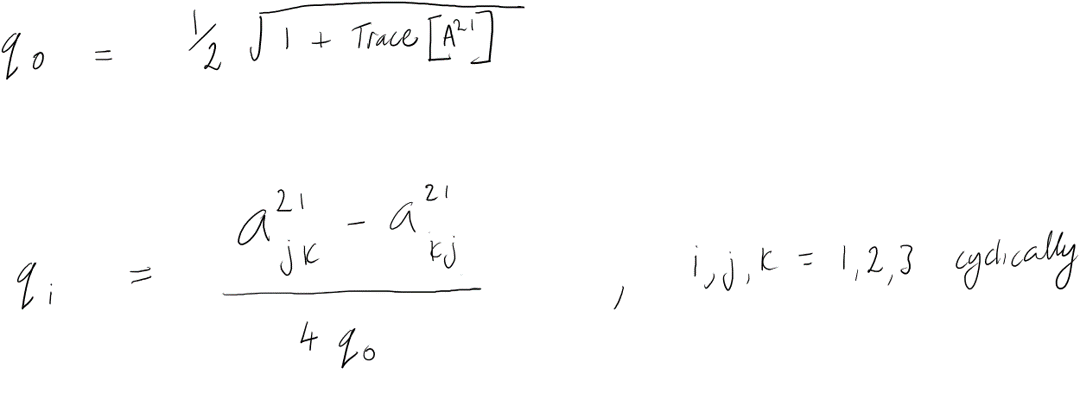
def EulRod(ROTM):
""" Find the Euler-Rodrigues parameters associated with a rotation matrix"""
q=[]
q.append((1/2)*sqrt(1+(np.trace(ROTM))))
q.append(np.array(ROTM[1][2]-ROTM[2][1])/(4*q[0]))
q.append(np.array(ROTM[2][0]-ROTM[0][2])/(4*q[0]))
q.append(np.array(ROTM[0][1]-ROTM[1][0])/(4*q[0]))
return q
def q_conjugate(q):
w, x, y, z = q
return (w, -x, -y, -z)
def qv_mult(q1, v1):
q2 = [0, v1[0], v1[1], v1[2]]
q1=Quaternion(q1)
q1=q1.inverse
return q_mult(q_mult(q1, q2), q_conjugate(q1))[1:]
def q_mult(q1, q2):
w1, x1, y1, z1 = q1
w2, x2, y2, z2 = q2
w = w1 * w2 - x1 * x2 - y1 * y2 - z1 * z2
x = w1 * x2 + x1 * w2 + y1 * z2 - z1 * y2
y = w1 * y2 + y1 * w2 + z1 * x2 - x1 * z2
z = w1 * z2 + z1 * w2 + x1 * y2 - y1 * x2
return w, x, y, z
A21 = np.array([[0.3584,0.8613,-0.3603],[-0.6638,0.5064,0.5503],[0.6564,0.0420,0.7532]])
q=np.array(EulRod(A21))
print('Q3 answer:', q)
# Perform the rotation using Euler Rodrigues parameters and plot
fig = plt.figure(3)
ax = fig.add_subplot(111, projection='3d')
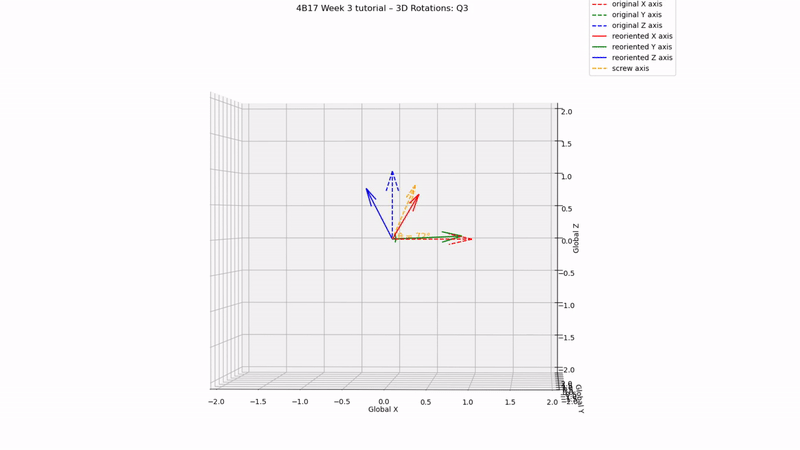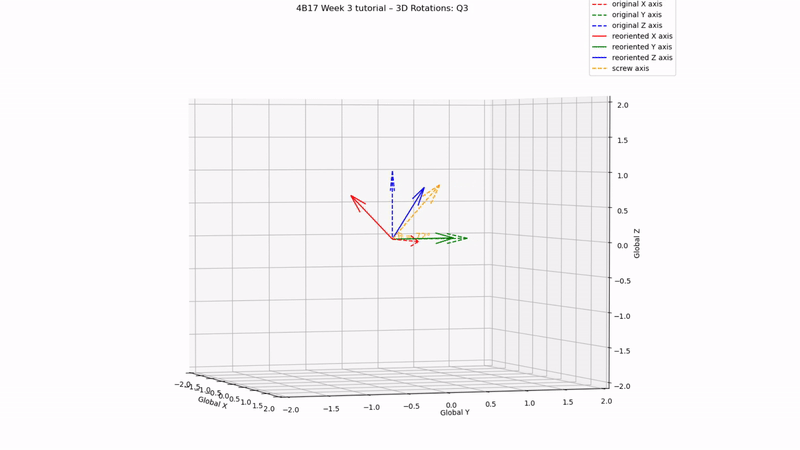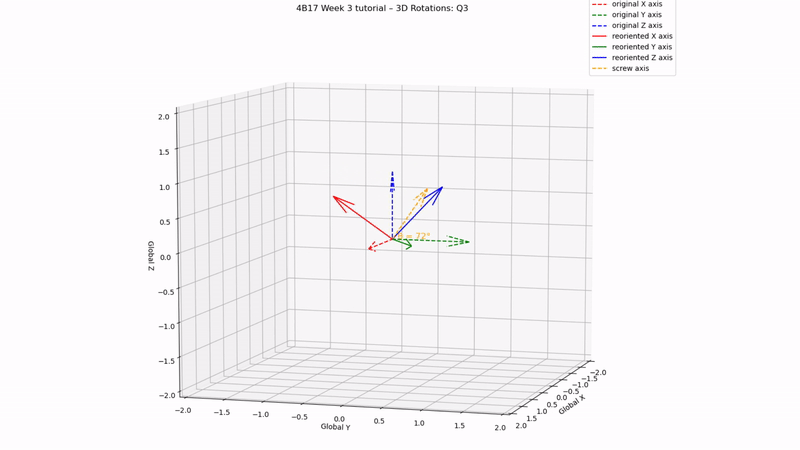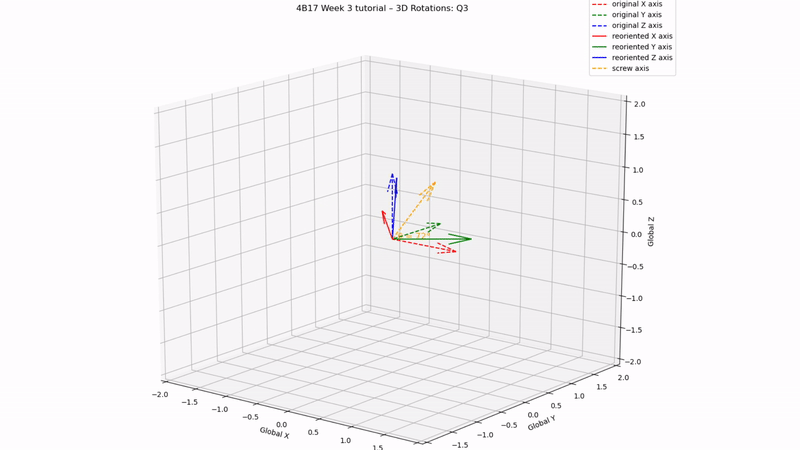
fig.suptitle('4B17 Week 3 tutorial – 3D Rotations: Q3', fontsize=12)
dirxlocal=[1,0,0]
dirylocal=[0,1,0]
dirzlocal=[0,0,1]
ax.quiver(0,0,0,dirxlocal[0],dirxlocal[1],dirxlocal[2],color='r',linestyle='--',label='original X axis')
ax.quiver(0,0,0,dirylocal[0],dirylocal[1],dirylocal[2],color='g',linestyle='--',label='original Y axis')
ax.quiver(0,0,0,dirzlocal[0],dirzlocal[1],dirzlocal[2],color='b',linestyle='--',label='original Z axis')
# q'/(q*q')
dirxlocal=qv_mult(q,[1,0,0])
dirylocal=qv_mult(q,[0,1,0])
dirzlocal=qv_mult(q,[0,0,1])
ax.quiver(0,0,0,dirxlocal[0],dirxlocal[1],dirxlocal[2],color='r',label='reoriented X axis')
ax.quiver(0,0,0,dirylocal[0],dirylocal[1],dirylocal[2],color='g',label='reoriented Y axis')
ax.quiver(0,0,0,dirzlocal[0],dirzlocal[1],dirzlocal[2],color='b',label='reoriented Z axis')
# Plot screw axis and angle
ax.quiver(0,0,0,n[0],n[1],n[2],color='orange',linestyle='--',label='screw axis')
ax.text(0,0,0, ' θ = '+str(round(np.degrees(θ)))+'°', size=12, zorder=1,color='orange')
# Axis limits and lables and legend
ax.set_xlim3d(-2,2)
ax.set_ylim3d(-2,2)
ax.set_zlim3d(-2,2)
ax.set_xlabel('Global X')
ax.set_ylabel('Global Y')
ax.set_zlabel('Global Z')
ax.legend()
plt.show()
Q3 answer:
[0.81, 0.16, 0.31, 0.47]
Q4
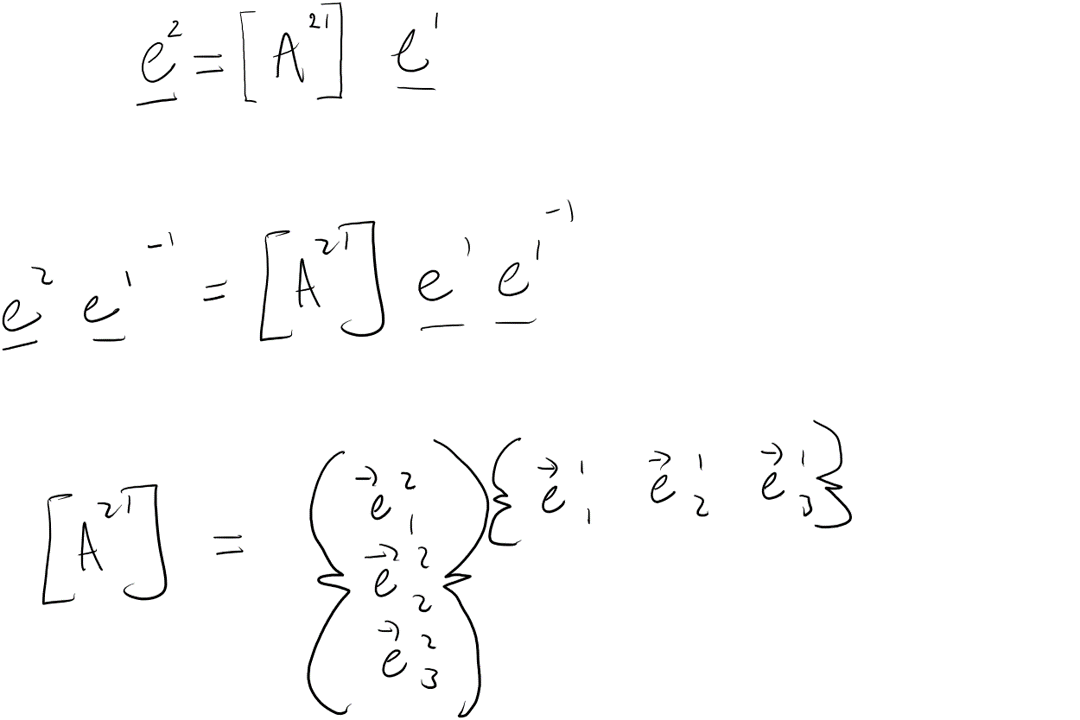
Q5
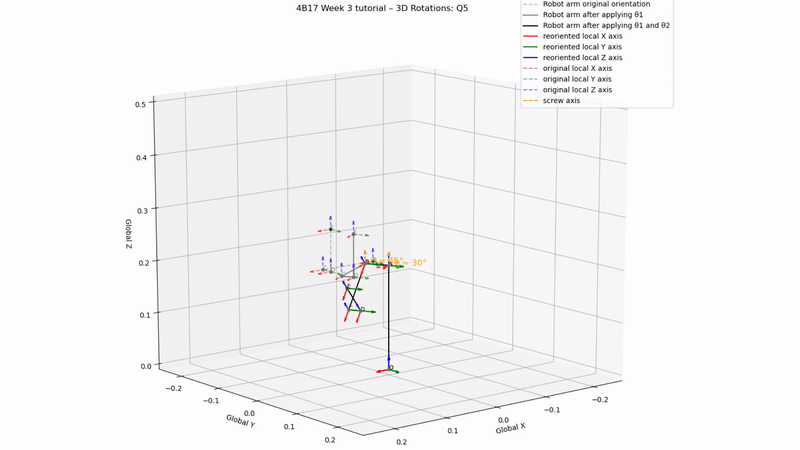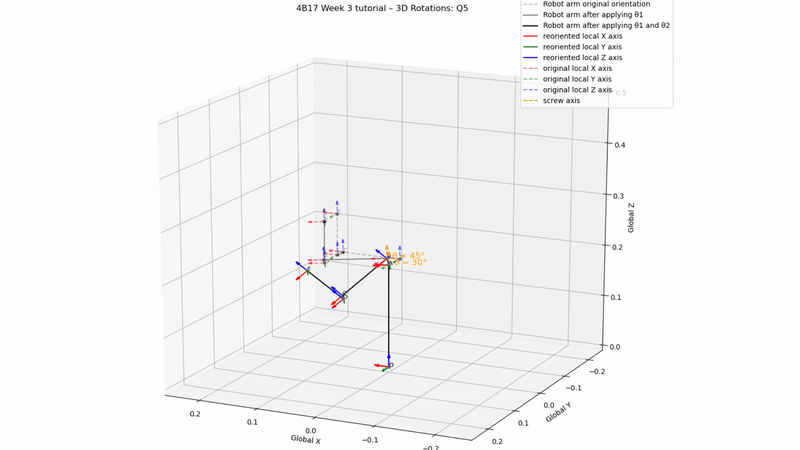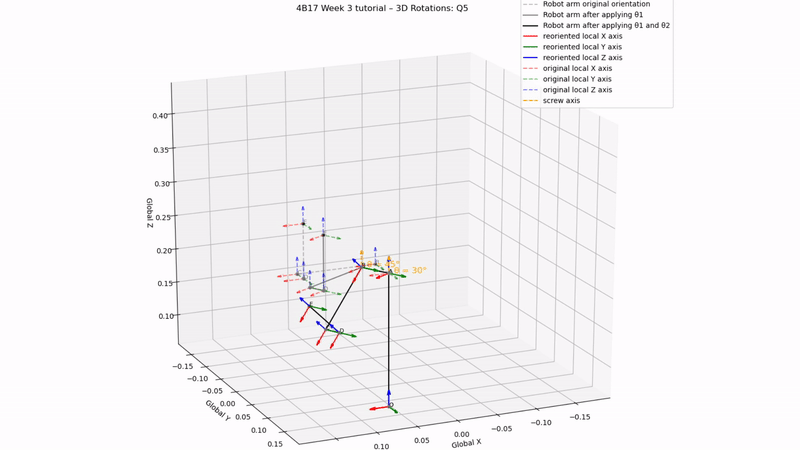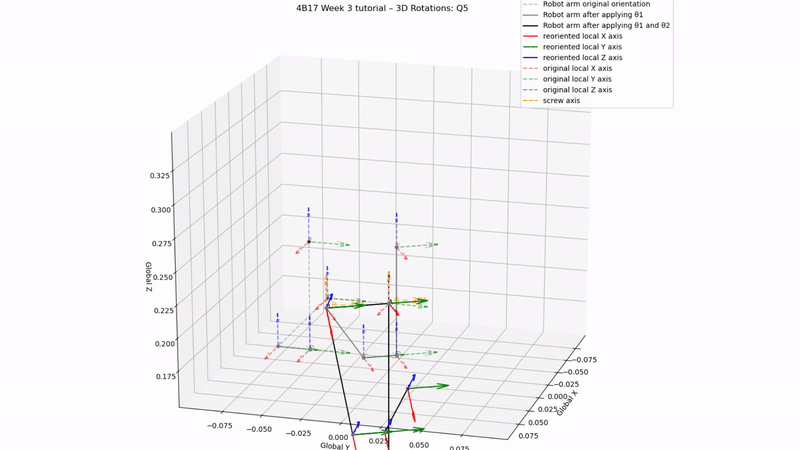
a)
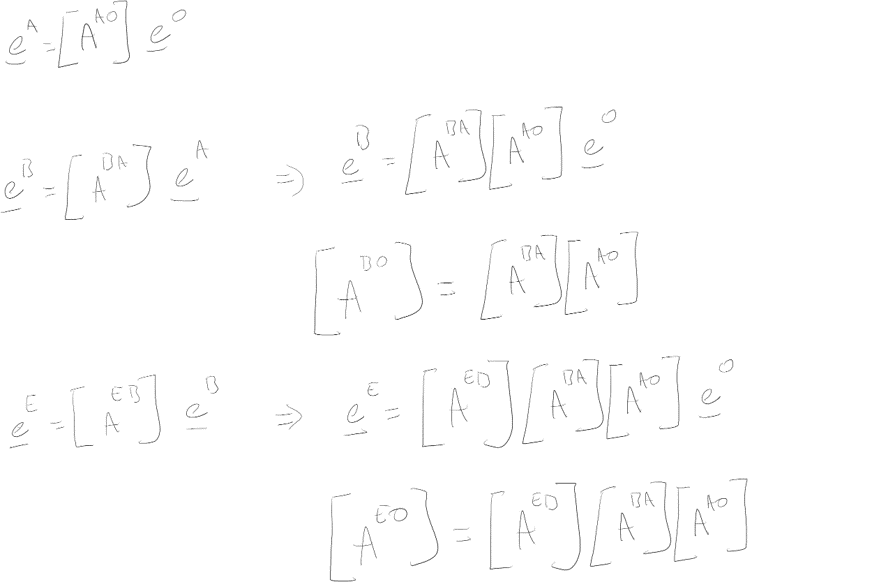
b)
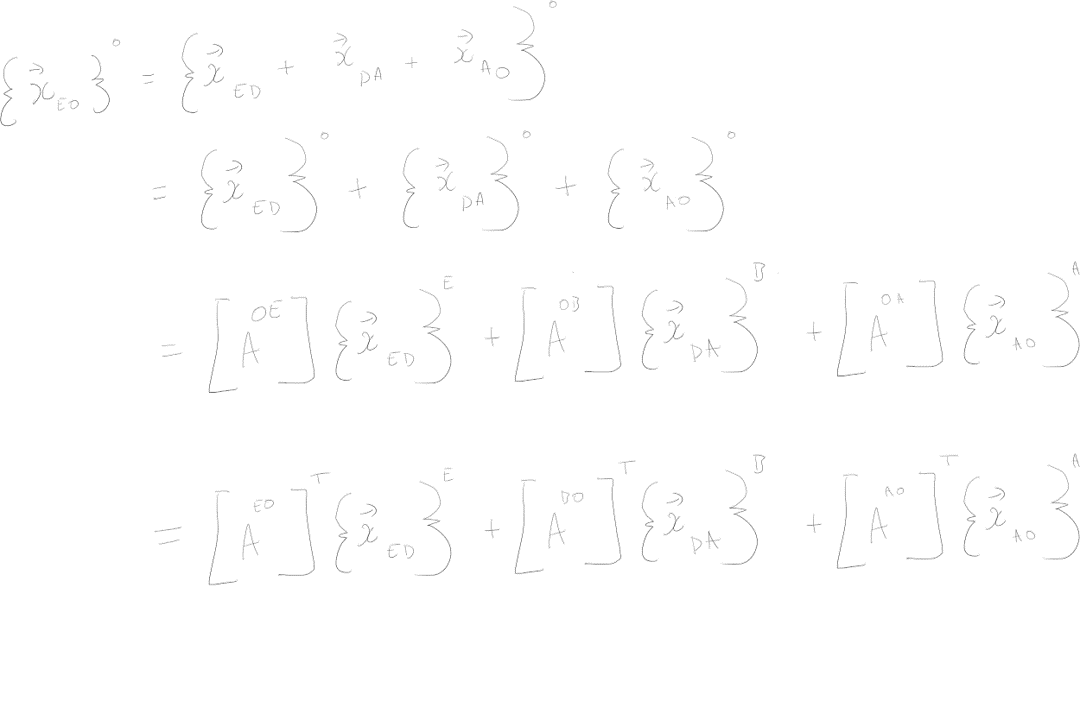
# Necessary functions for forward kinematics
def jnt_path(graph, start, end, path=[]):
path = path + [start]
if start == end:
return path
if not start in graph:
return None
for node in graph[start]:
if node not in path:
newpath = jnt_path(graph, node, end, path)
if newpath: return newpath
return None
def takeSecond(elem):
return elem[1]
def parent_child(graph):
parent_child_pairs = []
for i in range(max(graph[max(graph)])+1):
for j in range(max(graph[max(graph)])+1):
pair = jnt_path(dir_graph, i, j)
if pair != None:
if len(pair)==2:
parent_child_pairs.append(pair)
parent_child_pairs.sort(key=takeSecond)
return parent_child_pairs
def FK_local2global(chain,dir_graph):
""" perform forward kinematics to to convert joint orientations and position vectors into the global coordinate system"""
ref_space_ori = np.array([[1, 0, 0],
[0, 1, 0],
[0, 0, 1]])
ref_space_pos = np.array([0, 0, 0])
oris=[]
poss=[]
for i in range (len(chain)):
path = jnt_path(dir_graph, 0, i)
ori = ref_space_ori
pos = ref_space_pos
for j in path:
pos=pos + ori @ chain[j][2]
ori=ori @ chain[j][1]
oris.append(ori)
poss.append(pos)
return oris, poss
def RotationY(θy):
""" Calculate a rotation matrix for a rotation about the Y axis"""
ROTMy = np.array([[np.cos(θy),0,-np.sin(θy)],
[0,1,0],
[np.sin(θy),0,np.cos(θy)]])
return ROTMy
def RotationZ(θz):
""" Calculate a rotation matrix for a rotation about the Z axis"""
ROTMy = np.array([[np.cos(θz),np.sin(θz),0],
[-np.sin(θz),np.cos(θz),0],
[0,0,1]])
return ROTMy
# Define the Kinematic chain using local orientations (relative to parent) as 3x3 rotation matrices, and local position offset vectors (position of child relative to parent)
chain=[]
chain.append(['O', np.array([[ 1, 0, 0],
[ 0, 1, 0],
[ 0, 0, 1]]),
np.array([0,0,0])])
chain.append(['A', np.array([[ 1, 0, 0],
[ 0, 1, 0],
[ 0, 0, 1]]),
np.array([0,0,0.2])])
chain.append(['B', np.array([[ 1, 0, 0],
[ 0, 1, 0],
[ 0, 0, 1]]),
np.array([0,-0.04,0])])
chain.append(['C', np.array([[ 1, 0, 0],
[ 0, 1, 0],
[ 0, 0, 1]]),
np.array([0.1,0,0])])
chain.append(['D', np.array([[ 1, 0, 0],
[ 0, 1, 0],
[ 0, 0, 1]]),
np.array([0,0.02,0])])
chain.append(['E', np.array([[ 1, 0, 0],
[ 0, 1, 0],
[ 0, 0, 1]]),
np.array([0,0,0.08])])
# a directed graph with parent/child relationship knowledge is needed for constructing the kinematic chain
dir_graph = {0: [1],
1: [2],
2: [3],
3: [4],
4: [5]}
# find parent/child pairs from the directed graph
parent_child_pairs=parent_child(dir_graph)
# apply forward kinematics
ori, pos = FK_local2global(chain,dir_graph)
# Plot the kinematic chain
fig = plt.figure(5)
ax = fig.add_subplot(111, projection='3d')
fig.suptitle('4B17 Week 3 tutorial – 3D Rotations: Q5', fontsize=12)
dirxlocal=[1,0,0]
dirylocal=[0,1,0]
dirzlocal=[0,0,1]
ax.quiver(0,0,0,dirxlocal[0],dirxlocal[1],dirxlocal[2],length=0.025,color='r',label='reoriented local X axis')
ax.quiver(0,0,0,dirylocal[0],dirylocal[1],dirylocal[2],length=0.025,color='g',label='reoriented local Y axis')
ax.quiver(0,0,0,dirzlocal[0],dirzlocal[1],dirzlocal[2],length=0.025,color='b',label='reoriented local Z axis')
ax.quiver(0,0,0,dirxlocal[0],dirxlocal[1],dirxlocal[2],length=0.025,color='r',label='original local X axis',linestyle='--', alpha=0.5)
ax.quiver(0,0,0,dirylocal[0],dirylocal[1],dirylocal[2],length=0.025,color='g',label='original local Y axis',linestyle='--', alpha=0.5)
ax.quiver(0,0,0,dirzlocal[0],dirzlocal[1],dirzlocal[2],length=0.025,color='b',label='original local Z axis',linestyle='--', alpha=0.5)
x=[]
y=[]
z=[]
for i in range(len(pos)):
x.append(pos[i][0])
y.append(pos[i][1])
z.append(pos[i][2])
dirxlocal=ori[i]@[1,0,0]
dirylocal=ori[i]@[0,1,0]
dirzlocal=ori[i]@[0,0,1]
ax.quiver(x[i],y[i],z[i],dirxlocal[0],dirxlocal[1],dirxlocal[2],length=0.025,color='r',linestyle='--', alpha=0.5)
ax.quiver(x[i],y[i],z[i],dirylocal[0],dirylocal[1],dirylocal[2],length=0.025,color='g',linestyle='--', alpha=0.5)
ax.quiver(x[i],y[i],z[i],dirzlocal[0],dirzlocal[1],dirzlocal[2],length=0.025,color='b',linestyle='--', alpha=0.5)
ax.scatter(x, y, z, c=['gray']*len(chain), marker='o')
for i in range(len(chain)):
ax.scatter(x[i], y[i], z[i], c='black', marker='.')
ax.text(x[i], y[i], z[i], '%s' % (str(chain[i][0])), size=8, zorder=1,color='gray')
for j in range(len(parent_child_pairs)):
xs = [x[parent_child_pairs[j][0]],x[parent_child_pairs[j][1]]]
ys = [y[parent_child_pairs[j][0]],y[parent_child_pairs[j][1]]]
zs = [z[parent_child_pairs[j][0]],z[parent_child_pairs[j][1]]]
line = plt3d.art3d.Line3D(xs, ys, zs, c='gray',linestyle='--',alpha=0.5)
ax.add_line(line)
# Rotations we want to apply
θ1 = 30
θ2 = 45
θ3 = 0
# apply Q1 to the robot
chain[1][1]=RotationZ(np.radians(θ1)).T @ chain[1][1]
# apply forward kinematics
ori, pos = FK_local2global(chain,dir_graph)
x=[]
y=[]
z=[]
for i in range(len(pos)):
x.append(pos[i][0])
y.append(pos[i][1])
z.append(pos[i][2])
dirxlocal=ori[i]@[1,0,0]
dirylocal=ori[i]@[0,1,0]
dirzlocal=ori[i]@[0,0,1]
ax.quiver(x[i],y[i],z[i],dirxlocal[0],dirxlocal[1],dirxlocal[2],length=0.025,color='r',linestyle='--',alpha=0.5)
ax.quiver(x[i],y[i],z[i],dirylocal[0],dirylocal[1],dirylocal[2],length=0.025,color='g',linestyle='--',alpha=0.5)
ax.quiver(x[i],y[i],z[i],dirzlocal[0],dirzlocal[1],dirzlocal[2],length=0.025,color='b',linestyle='--',alpha=0.5)
ax.scatter(x, y, z, c=['gray']*len(chain), marker='o')
for i in range(len(chain)):
ax.scatter(x[i], y[i], z[i], c='black', marker='.')
ax.text(x[i], y[i], z[i], '%s' % (str(chain[i][0])), size=8, zorder=1,color='gray')
for j in range(len(parent_child_pairs)):
xs = [x[parent_child_pairs[j][0]],x[parent_child_pairs[j][1]]]
ys = [y[parent_child_pairs[j][0]],y[parent_child_pairs[j][1]]]
zs = [z[parent_child_pairs[j][0]],z[parent_child_pairs[j][1]]]
line = plt3d.art3d.Line3D(xs, ys, zs,color='gray')
ax.add_line(line)
# Plot screw axis and angle
θ,n = Screw(RotationZ(np.radians(θ1)))
line = plt3d.art3d.Line3D(xs, ys, zs, color='orange',linestyle='--',alpha=0.5)
ax.quiver(pos[1][0],pos[1][1],pos[1][2],n[0],n[1],n[2],length=0.025,color='orange',linestyle='--')
ax.text(pos[1][0],pos[1][1],pos[1][2], ' θ = '+str(round(np.degrees(θ)))+'°', size=12, zorder=1,color='orange')
# apply θ2 to the robot
chain[2][1]=RotationY(np.radians(θ2)).T @ chain[2][1]
# apply forward kinematics
ori, pos = FK_local2global(chain,dir_graph)
x=[]
y=[]
z=[]
for i in range(len(pos)):
x.append(pos[i][0])
y.append(pos[i][1])
z.append(pos[i][2])
dirxlocal=ori[i]@[1,0,0]
dirylocal=ori[i]@[0,1,0]
dirzlocal=ori[i]@[0,0,1]
ax.quiver(x[i],y[i],z[i],dirxlocal[0],dirxlocal[1],dirxlocal[2],length=0.025,color='r')
ax.quiver(x[i],y[i],z[i],dirylocal[0],dirylocal[1],dirylocal[2],length=0.025,color='g')
ax.quiver(x[i],y[i],z[i],dirzlocal[0],dirzlocal[1],dirzlocal[2],length=0.025,color='b')
ax.scatter(x, y, z, c=['gray']*len(chain), marker='o')
for i in range(len(chain)):
ax.scatter(x[i], y[i], z[i], c='black', marker='.')
ax.text(x[i], y[i], z[i], '%s' % (str(chain[i][0])), size=8, zorder=1,color='black')
for j in range(len(parent_child_pairs)):
xs = [x[parent_child_pairs[j][0]],x[parent_child_pairs[j][1]]]
ys = [y[parent_child_pairs[j][0]],y[parent_child_pairs[j][1]]]
zs = [z[parent_child_pairs[j][0]],z[parent_child_pairs[j][1]]]
line = plt3d.art3d.Line3D(xs, ys, zs, c='black')
ax.add_line(line)
# Plot screw axis and angle
θ,n = Screw(RotationZ(np.radians(θ2)))
line = plt3d.art3d.Line3D(xs, ys, zs, color='orange',linestyle='--',alpha=0.5)
ax.quiver(pos[2][0],pos[2][1],pos[2][2],n[0],n[1],n[2],length=0.025,color='orange',linestyle='--')
ax.text(pos[2][0],pos[2][1],pos[2][2], ' θ = '+str(round(np.degrees(θ)))+'°', size=12, zorder=1,color='orange')
# Axis limits and lables
ax.set_xlim3d(-0.25,0.25)
ax.set_ylim3d(-0.25,0.25)
ax.set_zlim3d(0,0.5)
ax.set_xlabel('Global X')
ax.set_ylabel('Global Y')
ax.set_zlabel('Global Z')
line = plt3d.art3d.Line3D([0,0], [0,0], [0,0], c='gray',linestyle='--',alpha=0.5,label='Robot arm original orientation')
ax.add_line(line)
line = plt3d.art3d.Line3D([0,0], [0,0], [0,0], c='gray',label='Robot arm after applying θ1')
ax.add_line(line)
line = plt3d.art3d.Line3D([0,0], [0,0], [0,0], c='black',label='Robot arm after applying θ1 and θ2')
ax.add_line(line)
ax.quiver(pos[1][0],pos[1][1],pos[1][2],n[0],n[1],n[2],length=0.025,color='orange',linestyle='--',label='screw axis')
ax.legend()
# Part a)
print('Q5 a) answer:', ori[-1].T)
# Part b)
print('Q5 b) answer:', pos[-1])
plt.show()
Q5 a) answer:
[[0.61 0.35 -0.71] [-0.5 0.89 0.00] [0.61 0.35 0.71]]
Q5 b) answer: [0.12 0.05 0.19]
Q5 b) check
def RotationY(θy):
""" Calculate a rotation matrix for a rotation about the Y axis"""
ROTMy = np.array([[np.cos(θy),0,-np.sin(θy)],
[0,1,0],
[np.sin(θy),0,np.cos(θy)]])
return ROTMy
def RotationZ(θz):
""" Calculate a rotation matrix for a rotation about the Z axis"""
ROTMy = np.array([[np.cos(θz),np.sin(θz),0],
[-np.sin(θz),np.cos(θz),0],
[0,0,1]])
return ROTMy
# Approach 1
A3 = RotationY(np.radians(θ3)).T
A2 = RotationY(np.radians(θ2)).T
A1 = RotationZ(np.radians(θ1)).T
print('Approach 1:', A1@A2@A3@np.array([0,0,0.08])+A1@A2@np.array([0.1,-0.02,0])+A1@np.array([0,0,0.2]))
# Approach 2
A3 = RotationY(np.radians(θ3))
A2 = RotationY(np.radians(θ2))
A1 = RotationZ(np.radians(θ1))
print('Approach 2:', (A3@A2@A1).T@np.array([0,0,0.08])+(A2@A1).T@np.array([0.1,-0.02,0])+(A1).T@np.array([0,0,0.2]))
Approach 1: [0.12 0.05 0.19]
Approach 2: [0.12 0.05 0.19]
